Introduction | Example | Tutorial | Applications

Introduction - Trapezoidal Rule Excel

Use this Trapezoidal Rule Excel Function to approximate the definite integral of paired data sets. A VBA Excel function to find the area under a curve is useful in engineering, business, finance and many scientific fields.

The trapezoidal rule is one of several ways to perform numerical integration on raw data. This tutorial will show you how to use the trapezoidal rule in Excel.

Example - Trapezoidal Rule Excel

Trapezoidal Rule Excel Function

Function TrapIntegration(KnownXs As Variant, KnownYs As Variant) As Variant
'------------------------------------------------------------------------------------------------------
'---DESCRIPTION: Approximates the integral using trapezoidal rule.-------------------------------------
'---CREATED BY: Ryan Wells-----------------------------------------------------------------------------
'---INPUT: KnownXs is the range of x-values. KnownYs is the range of y-values.-------------------------
'---OUTPUT: The output will be the approximate area under the curve (integral).------------------------
'------------------------------------------------------------------------------------------------------

    Dim i As Integer
    Dim bYrows As Boolean, bXrows As Boolean

'------------------------------------------------------------------------------
'I. Preliminary Error Checking
'------------------------------------------------------------------------------
On Error GoTo TrapIntError:
    'Error 1 - Check if the X values are range.
    If Not TypeName(KnownXs) = "Range" Then
        TrapIntegration = "Invalid X-range"
        Exit Function
    End If

    'Error 2 - Check if the Y values are range.
    If Not TypeName(KnownYs) = "Range" Then
        TrapIntegration = "Invalid Y-range"
        Exit Function
    End If


    'Error 3 - dimensions aren't even
    If KnownYs.Count <> KnownXs.Count Or _
       KnownYs.Rows.Count <> KnownXs.Rows.Count Or _
       KnownYs.Columns.Count <> KnownXs.Columns.Count Then
        TrapIntegration = "Known ranges are different dimensions."
        Exit Function
    End If
     
    'Error 4 - known Ys are not Nx1 or 1xN dimensions
    If KnownYs.Rows.Count <> 1 And KnownYs.Columns.Count <> 1 Then
        TrapIntegration = "Known Y's should be in a single column or a single row."
        Exit Function
    End If
     
    'Error 5 - known Xs are not Nx1 or 1xN dimensions
    If KnownXs.Rows.Count <> 1 And KnownXs.Columns.Count <> 1 Then
        TrapIntegration = "Known X's should be in a single column or a single row."
        Exit Function
    End If
     
    'Error 6 - Check for non-numeric KnownYs
    If KnownYs.Rows.Count > 1 Then
        bYrows = True
        For i = 1 To KnownYs.Rows.Count
            If IsNumeric(KnownYs.Cells(i, 1)) = False Then
                TrapIntegration = "One or all Known Y's are non-numeric."
                Exit Function
            End If
        Next i
    ElseIf KnownYs.Columns.Count > 1 Then
        bYrows = False
        For i = 1 To KnownYs.Columns.Count
            If IsNumeric(KnownYs.Cells(1, i)) = False Then
                TrapIntegration = "One or all KnownYs are non-numeric."
                Exit Function
            End If
        Next i
    End If
     
    'Error 7 - Check for non-numeric KnownXs
    If KnownXs.Rows.Count > 1 Then
        bXrows = True
        For i = 1 To KnownXs.Rows.Count
            If IsNumeric(KnownXs.Cells(i, 1)) = False Then
                TrapIntegration = "One or all Known X's are non-numeric."
                Exit Function
            End If
        Next i
    ElseIf KnownXs.Columns.Count > 1 Then
        bXrows = False
        For i = 1 To KnownXs.Columns.Count
            If IsNumeric(KnownXs.Cells(1, i)) = False Then
                TrapIntegration = "One or all Known X's are non-numeric."
                Exit Function
            End If
        Next i
    End If

'------------------------------------------------------------------------------
'II. Perform Trapezoidal Integration
'------------------------------------------------------------------------------
    TrapIntegration = 0

    'Apply the trapezoid rule: (y(i+1) + y(i))*(x(i+1) - x(i))*1/2.
    'Use the absolute value in case of negative numbers.
    If bXrows = True Then
        For i = 1 To KnownXs.Rows.Count - 1
            TrapIntegration = TrapIntegration + Abs(0.5 * (KnownXs.Cells(i + 1, 1) _
            - KnownXs.Cells(i, 1)) * (KnownYs.Cells(i, 1) + KnownYs.Cells(i + 1, 1)))
        Next i
    Else
        For i = 1 To KnownXs.Columns.Count - 1
            TrapIntegration = TrapIntegration + Abs(0.5 * (KnownXs.Cells(1, i + 1) _
            - KnownXs.Cells(1, i)) * (KnownYs.Cells(1, i) + KnownYs.Cells(1, i + 1)))
        Next i
    End If
Exit Function

TrapIntError:
    TrapIntegration = "Error Encountered: " & Err.Number & ", " & Err.Description
End Function

Make powerful macros with our free VBA Developer Kit

It’s easy to copy and paste a macro like this, but it’s harder make one on your own. To help you make macros like this, we built a free VBA Developer Kit and wrote the Big Book of Excel VBA Macros full of hundreds of pre-built macros to help you master file I/O, arrays, strings and more - grab your free copy below.

I'll take a free VBA Developer Kit

Tutorial - Trapezoidal Rule Excel

  1. Excel Macro Tutorial
    1. Open Visual Basic for Applications Editor
      Two options
      1. Press “Alt+F11”
        or
      2. Click “Visual Basic” on the Developer tab.
    2. From the Editor, click “Insert” at the top, then “Module”
      1. You can rename the module in the Properties window, if you like.
        The default name is Module1
    3. Paste Trapezoidal Rule Excel Function example to the editor
    4. Save and exit the editor
  2. Use Trapezoidal Rule Excel Function

    1. From Excel, type =TrapIntegration(KnownXs, KnownYs) into a blank cell where KnownXs and KnownYs are the ranges of your x-axis data and y-axis data.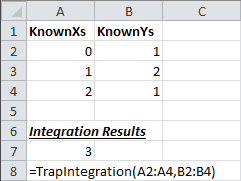

      Trapezoidal Rule Excel

In the above example, =TrapIntegration(A2:A4,B2:B4) performs numerical integration on the data to yield a result of 3.

Application Ideas - Trapezoidal Rule Excel

It’s a fruitless task to try to name the applications where the trapezoidal rule can be used. The possibilities are endless. You can use numerical integration to solve billions of problems. Any time you want to approximate the area under a curve, the trapezoidal rule can be used.

One example of where I used this trapezoidal rule excel function in my engineering job was to approximate the integral of LPRM (Local Power Range Monitor) responses for a nuclear plant. I used this an alternate means of characterizing the health of our control blades - a term we dubbed “Watt-Days.”

That’s all for this tutorial. When you’re ready to take your VBA to the next level, subscribe using the form below.